OCTAL
El codigo octal es un sistema de numeracion formada por 8 digitos 0 1 2 3 4 5 6 7 tambien se considera como un idioma del ordenador
Como pasar de binario a octal
El codigo octal funciona tambien por una tabla que nesecitaremos para poder convertir un
numero binario a octal de una manera mas facil y rapida, la tabla de binaria a octal
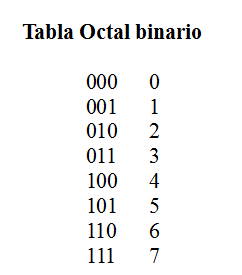
Esta tabla es como decir la "traduccion" de los numeros del sistema octal en el sistema binario.
Para entender como funciona analizaremos otra imagen
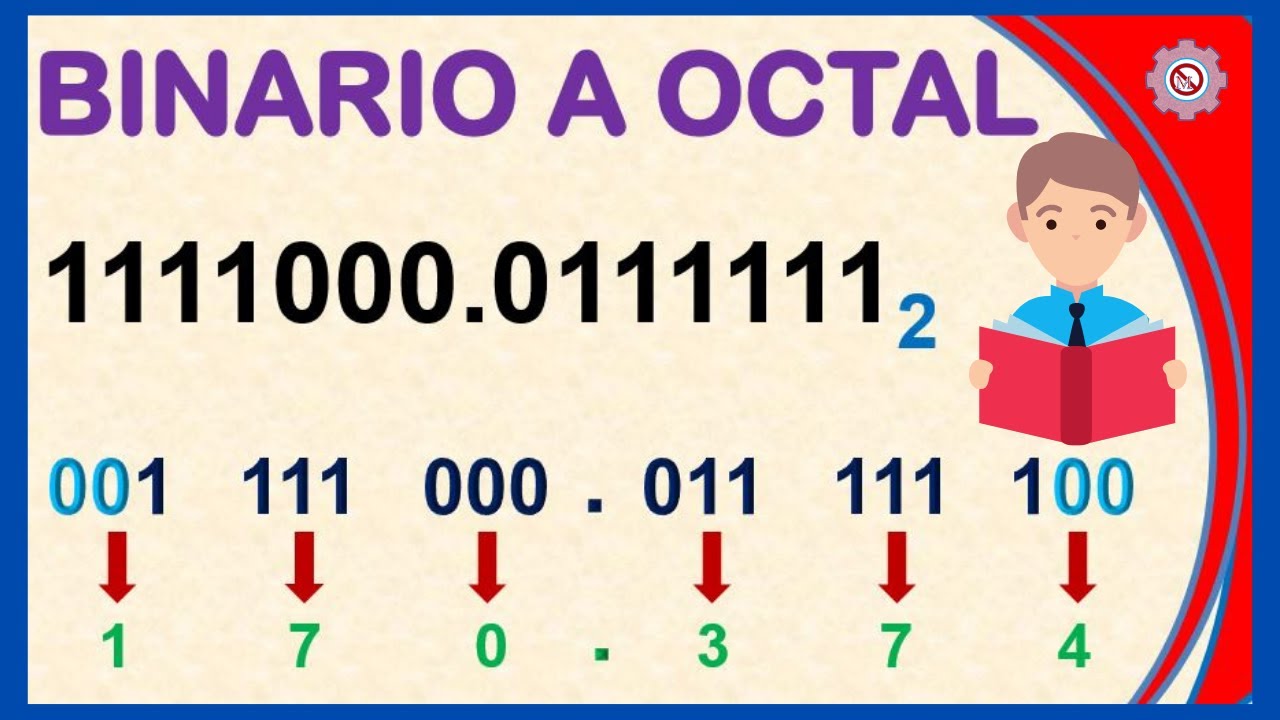
Tenemos 2 ejemplos el codigo 1111000 y 0111111, antes que todo tenemos que saber como funciona esta forma
de convertir un numero binario a octal
Explicacion
Este sistema de conversion consiste en agrupar 3 numeros binarios y con la ayuda de la tabla traducirlos
un ejemplo pequenyo "100101" segun la tabla el numero (100) en codigo octal significa (4) y el numero
(101) significa (5), entonces eso quiere decir que el resultado es 45.
Otra cosa tambien que hay que tener en cuenta es que cuando el numero binario no se agrupa de la manera correcta
osea que no hay suficientes numeros para agrupar de 3 en 3.
ejemplo pequenyo "1101001" (forma agrupada 1 101 001) aqui vemos que nos sobra 1 numeros que no se pueden agrupar de 3
que es el 1 ya que no tiene mas numeros para agruparse, lo que se hace en este caso es aumentar ceros hasta que se pueda agrupar
en este caso pondriamos 2 ceros junto al 1 que esta sin grupo, y con eso podriamos convertir el numero perfectamente, pero si
el resultado quedaria asi 001 101 001
lleva el elevado sobre 2 osea "1101001^2" los ceros que aumentariamos seria por el final osea (forma agrupada y con ceros añadidos 110 100 100)
Resolvimiento
Numero: 1111000 = (001 111 000) segun nuestra tabla de conversion: 001=1 111=7 000=0 de resultado nos daria= 170
Numero 0111111^2 =(111 111 100) segun nuestra tabla de conversion: 011=3 111=7 100=4 de resultado nos daria= 374
Como pasar de octal a binario
ya sabiendo lo anterior explicado sera muy facil resolver la siguiente imagen

La forma de resolverlo es la misma que lo ya explicado anteriormente pero al revez, lo unico que tenemos que
hacer es coger los numeros octales y con ayuda de la tabla de binario a octal traducirlo.
Resolvimiento
Numero 6215 = segun nuestra tabla de conversion 6=110 2=010 1=001 5=101 el resultado nos daria 110010001101
Hexadecimal
El codigo hexadecimal es un sistema de numeros pero tambien letras que llegan hasta el numero 15 pero sustituyendo
los numeros superiores al 9 por letras es decir: 0 1 2 3 4 5 6 7 8 9 A B C D E F
Como pasar de binario a hexadecimal
como todos los codigos anterioriores tambien utilizaremos 1 tabla
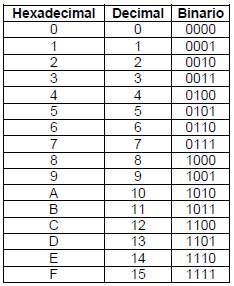
esta tabla nos ayudara a convertir un numero binario a decimal
analizaremos la siguiente imagen
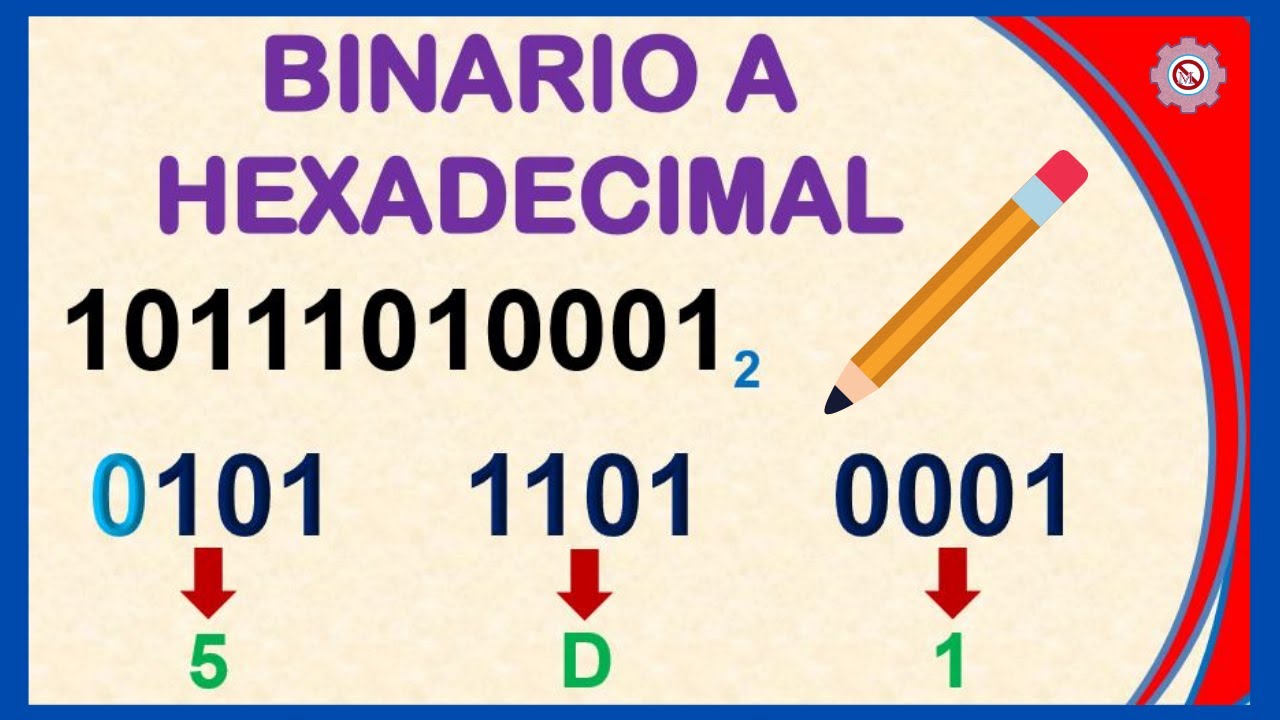
Vemos que es muy similar a como convertir de binario a octal, solo que ahora en vez de agrupar de 3 numeros
agrupamos de 4 numeros y sustituyendo por una letra los numeros superiores a 9
vemos que el numero que tenemos que resolver es: 10111010001^2
en este caso vemos que si agrupamos de 4 en 4 hay un grupo que se queda de 3 en este caso es lo contrario
que en octal, es decir que cuando esta elevado a 2 los ceros adicionales se ponen en el principio
en el codigo octal se ponia al final
Resolvimiento
10111010001= (agrupando seria (0101)(1101)(0001)) el 0 esta subrayado porque es el adicional
0101= segun nuestra tabla seria 5
1101= segun nuestra tabla seria 14, pero como en el codigo hexadecimal el 14 se sutituye por una D
0001= segun nuestra tabla seria 1
como nresultado nos daria que 10111010001 = 5D1
Como pasar de hexadecimal a binario
Es muy similar a la forma de convertir un numero binario a decimal solo que al revez.
Traducimos el codigo hexadecimal de la siguiente imagen:
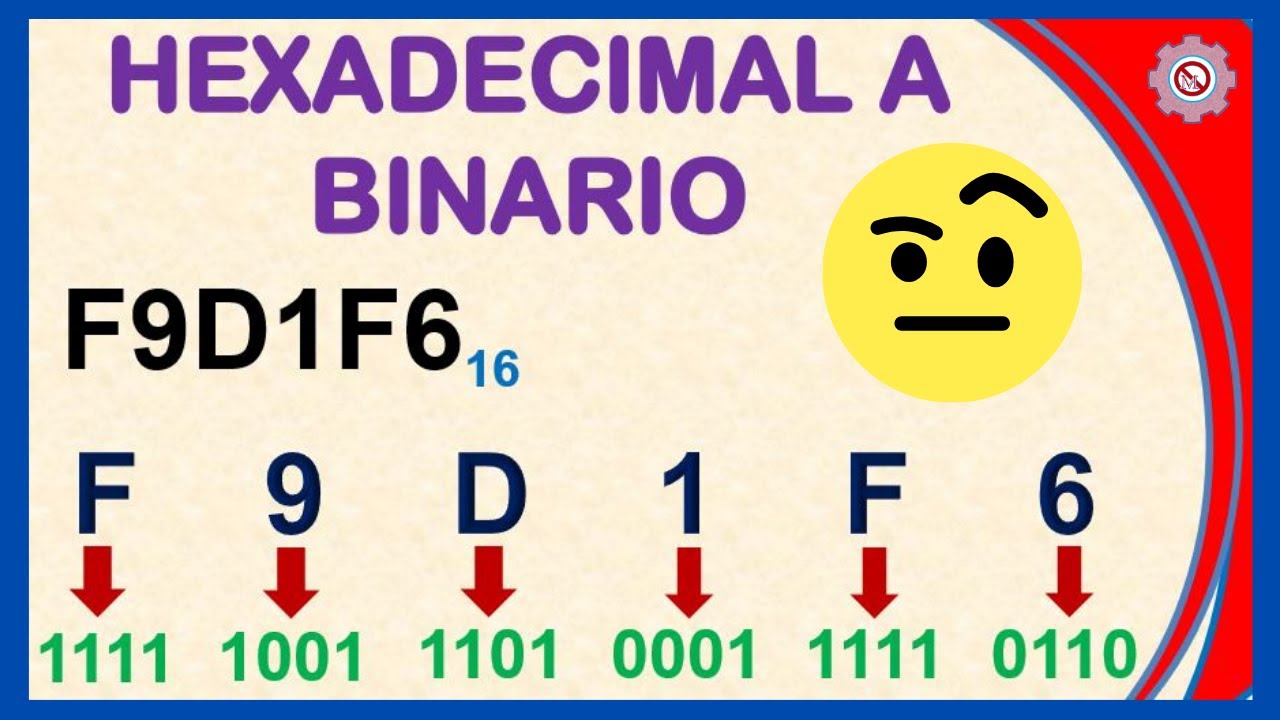
Es literalmente lo mismo que explique antes solo que al revez
Resultado
Codigo a resolver: F9D1F6
segun nuestra tabla F= 1111
segun nuestra tabla 9= 1001
segun nuestra tabla D= 1101
segun nuestra tabla 1= 0001
segun nuestra tabla F= 1111
segun nuestra tabla 6= 0110